More Gates
Now that we've mastered truth tables and the simple NOT, AND, and OR gates, we can construct more complicated gates.
NOR
The NOR gate is an OR followed by a NOT. This is written X=¬(A+B), or 
. Here, X is true only when neither A nor B is true. The NOR gate is drawn just like the OR gate except it has an empty dot tacked on the output (similar to the NOT gate).
The truth table for NOR is this (note that the third column is A OR B, so the last column is just the opposite of that):
 |  |  |  |
|---|---|---|---|
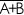| F | F | T | F |
| F | T | T | F |
| T | F | T | F |
| T | T | F | T |
NAND
The NAND gate is like NOR in that it is simply an AND followed by a NOT. This is written X=¬(AB), or 
. In the NAND gate X is true except when when when both A and B are true.
The truth table for NAND is:
| |  |  |
|---|---|---|---|
| F | F | F | T |
| F | T | F | T |
| T | F | F | T |
| T | T | T | F |
XOR
Exclusive Or, which is written as X=A
B, means "X is true if A or B is true but not if both are."
This gate can be created using other gates with the following configuration. Note that if there is not a solid dot where two wires cross, they do not touch but simply bypass each other. (Go ahead! Click on the circles on the left on this and the previous figure to convince yourself they have the same effect as the one above.)
The truth table for the XOR gate is seen below. See how the last column is simply the AND of the OR and NAND columns.
| | | | |
|---|---|---|---|---|
| F | F | F | T | F |
| F | T | T | T | T |
| T | F | T | T | T |
| T | T | T | F | F |
Multiple inputs
And finally, gates can be drawn as having more than two inputs.
This is in fact just a shorthand for a combination of gates. The above example of a three input OR gate is drawn as a single gate though it is made from two OR gates in sequence.
Next
So what practical purpose are these gates used for? Coming up we'll take a look at using these gates to do simple arithmetic. But first let's brush up on how to count in binary.
Next Up: Binary Numbers »
Further study
- Logic Gate on Wikipedia—another explanation of logic gates