Concept: Truth Tables
Truth tables are an easy way to define what a logical expression means. Basically they are a table where each column is an expression, and each row indicates if that expression is true (T) or false (F).
For example, I want to define a concept I'll call sunrain, as when it is raining and it is sunny. I'll construct a truth table for sunrain so that there is no doubt in what I mean.
| it is sunny | it is raining | it is sunrain |
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
As you can see this table doesn't tell me if it is really sunraining right now, but it defines in every possible situation, whether that situation should be called sunrain. So if I look at row 2, I see that if it is not sunny, though it is raining, it's false to say that it is sunrain.
Truth tables can help simpify a somewhat complex idea. In a more abstract sense, I can define X as true when "A AND B are true, or when B is not true, but C is true". So X = (A AND B) OR (NOT B AND C).
| A | B | C | A AND B | NOT B | NOT B AND C | (A AND B) OR (NOT B AND C) |
| F | F | F | F | T | F | F |
| F | F | T | F | T | T | T |
| F | T | F | F | F | F | F |
| F | T | T | F | F | F | F |
| T | F | F | F | T | F | F |
| T | F | T | F | T | T | T |
| T | T | F | T | F | F | T |
| T | T | T | T | F | F | T |
That's somewhat of a confusing definition, but just from a glance at the table we can see that X is true in four cases, and false in the other four. This table also helps in breaking down the definition, where each column builds on the previous columns, until the last one has the complete definition.
Below is a truth table of some basic expressions (which we'll talk about on later pages).
 |  |  | 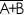 |  |  |    |  |  |  |  |    |
| F | F | F | T | F | T | F | T | T | T | T | F |
| F | T | T | F | F | T | T | T | F | T | F | T |
| T | F | T | F | F | T | T | F | T | T | F | T |
| T | T | T | F | T | F | F | F | F | F | F | F |
Next Up: More Gates »